the Mandelbrot Set with Base Tools in R

In this project, I wanted to play around with the very first fractal- Mandelbrot Set. Fractals are geometric shapes that when divided into parts, each part would be a smaller replica of the whole shape just like the atoms, or fiber in leaves, or the human dna. Fractals let us visualize nature in some sense. Of course, if you’re talking about fractals, then you have to start with the “father of fractals,” Dr. Benoit Mandelbrot. He was first to coin this bizarre term, and explained how we can mimic and see patterns in nature and even patterns present in cosmos. Anyways, let’s talk about how I drew this fractal.

Please feel free to look through the source code by going here.

A Mandelbrot is a set of numbers that display unusual properties. So, I started by making function that would generate those numbers by interating in a complex number plane (ps, don’t worry if your algeabric terminology is weak, I try my best to explain everything as I go), like this-

for(i in x){ 
  for(j in f(x)){
  # here we loop through the function 
  # that has complex numbers list
    f_x= mandelbrot(i,j) 
  # extra code
  }
}

The mandelbrot() function above contains an expression that creats set of numbers that behave differently if the x and y are between (-2, 1). Formally, F= {x^2 + c|x is any number, and -2< x <1} in a proper code form I have something like this-

mandelbrot <<- function(i,j){
  # extra code
  x <- i-c # here c is some real number
  y <- c-j 
  a <- complex(real = x/200, imaginary = y/200) #real numbers
  b <- complex(real = 0, imaginary = 0) #imaginary numbers
  # extra code
  b <- b*b+a  # expression
  # extra code
}

The reason why unusual properties occur between -2 and 1 is due to two simple rules of algebra-

1. Product of two negative numbers is a positive number.
2. Adding a negative is similar to subtracting that number’s positive value.

These two rules work against each other, so when we have the expression F= {x^2 + c|x is any number, and -2< x <1} and we iterate many complex numbers over this expression under the limit (-2,1), then we see sort of chaotic behaviour, where the output bounces back between a small segment of a number line, never going too far from 0, and never hitting the exact same value twice.

Because real numbers get exponentially large, we can use the complex numbers. Complex numbers do not sit on the number line, thus preventing us from an infinite sequence.

A complex number is basically a real number added to an imaginary number. Imaginary numbers are not really imaginary, they have to follow the same underlying rule as the real numbers. So, when we add the two together, the result is not real nor imaginary, it is complex.

Anyhow, getting back on the track, since complex numbers don’t really work well with 0s and 1s binaries, we have to convert the complex numbers to their standard form of expression by factoring out the -1. For example-

Solve: 2 + sqrt(-9)
=> 2 + sqrt(9 * -1)
=> 2 + sqrt(9) * sqrt(-1)
=> 2 + 3 * sqrt(-1)
=> 2 + 3i

So, whenever the complex numbers are broken down in \(Z= A+Bi\) form, they can be easily used in a calculation and get ordered in the complex plane.

A complex plane is just a 2-D extension of a real number plane, where the X-axis is a real number line, and Y-axis is an imaginary line (which mimics like a real number line). In the complex plane, each complex number has its unique address like (1, 1+1i), (1, 1+2i) and so on.

In code, this is how I am doing-

mandelbrot <<- function(i,j){
 # extra code
  x <- i-c 
  y <- c-j 
  a <- complex(real = x/200, imaginary = y/200) #real numbers
  b <- complex(real = 0, imaginary = 0) #imaginary numbers
  
  for(...){
    b <- b*b+a # iterate over expression
    # extra code
    }
  }
 # extra code
}

Therefore whenever any number that resides between (-2,1), in a complex plane that doesn’t cause an exponential growth, and become a circle with radius 2.

In the graph below, this nature is in black region-

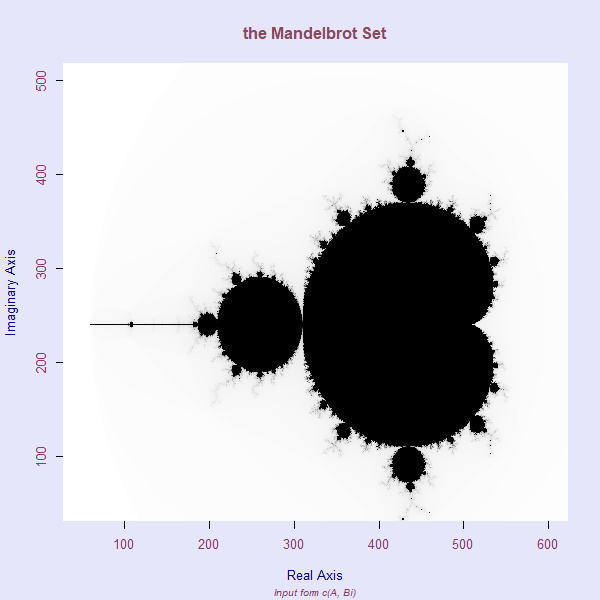
Now you might be wondering, why is there varying, sort of pear-like patterns, colour hue around the black region (you may have to zoom in)? In a nutshell, the region with similar colour is consisted of the numbers that have escaped the black region. Meaning, they are all the numbers which are part of the set F= {x^2 + c|x is any number, and -2< x <1} with given iteration. As we increased the iterations, we get more and more numbers escaping, thus creating the Mandelbrot fractal.

Even though code for this looks small (and unoptimized), it took 4-5 hrs to get the graph done. If you liked this post, and want to learn more about Mandelbrot Set, please go here to read more about them.

NOTE: Thank you very much for reading! If you discover any mistakes or want to offer any feedback, please feel free to email me.