Julia Sets and the Mandelbrot Family

Most popular fractals are variations of the Mandelbrot Set, sharing the same fundamental equation:

F = {x² + c| c is a constant, x is an iterated number}

If you would like to see the source code, you can find it here!

Meet the Julia Set

Named after Dr. Gaston Julia, Julia Sets represent a family of fractals that showcase nature’s intricate patterns. Let’s explore how they differ from their famous cousin, the Mandelbrot Set.

The Mathematical Dance

The key difference lies in how we handle the constants:

• Mandelbrot Set: We substitute different values of c from the complex plane, using each result as the next x
• Julia Set: We keep c fixed and vary our starting point Z₀, creating unique patterns with each chosen constant

Here’s how we implement this in R:

# Complex parameter, connected to coordinate of the Mandelbrot set in a complex plane
a <- -0.4
b <- -0.6

#coloring code....

#fixed numbers of steps
steps <- seq(fixed_limits[1], fixed_limits[2], by= 0.01)

#We keep each point in the array/matrix
points_matrix <- array(0, dim= c(length(steps) * length(steps), 3))

a1 <- 0

for(x in steps) {
  for(y in steps) {
    n <- 0
    distance <- 0
    # Copy original x and y
    x1 <- x
    y1 <- y 
      
      #This distance limit specific
      while(n < max_iteration & distance<4) {
        newx <- x1^2 - y1^2 + a
        newy <- 2 * x1 * y1 + b
        distance <- newx^2 + newy^2
        x1 <- newx
        y1 <- newy
        n <- n+1
      }
    
    if(distance < 4){
      #We pick the color for the number not in the step
      pick_color <- 24
    }
    else{
      #We pick the color for the number not in the step
      pick_color <- n*10 
    }
    
    a1 <- a1 + 1 #Next number
    points_matrix[a1, ]= c(x,y, pick_color)
    
  }
}

# plot() code.

The Beauty of Variation

Different values of c create dramatically different patterns:

1. Zn= x^2 +(-0.4+(-0.6i))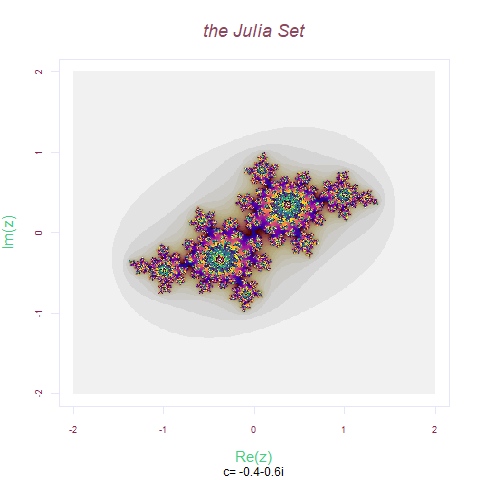

   

2. Zn= x^2 +(0+0.8i)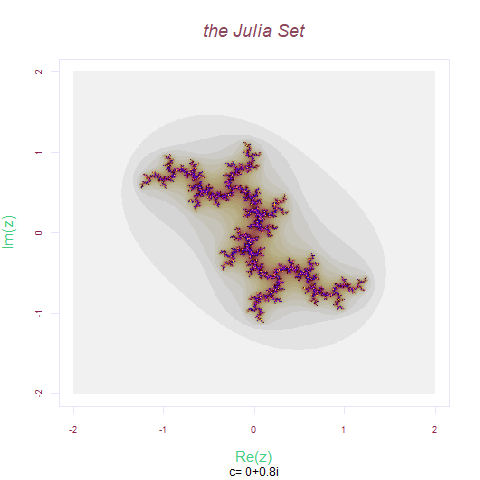

   

3. Zn= x^2 +(-0.34+ (-0.9i))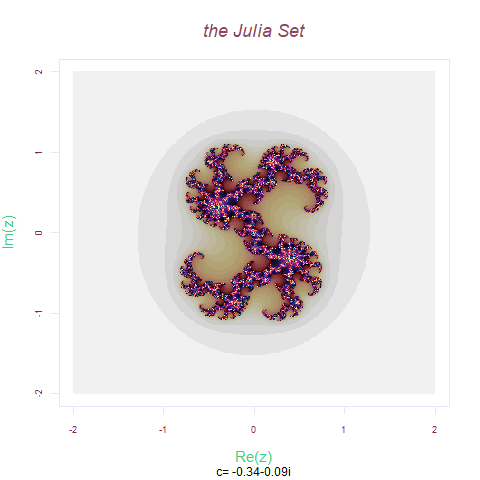

   

4. Zn= x^2 +(0.355+ 0.355i)

   

The Hidden Connection

Each endpoint of the Mandelbrot Set’s black region represents a potential value of c that generates a unique Julia Set. This deep connection suggests a profound truth, which is, these seemingly different patterns are intimately linked, much like the interconnected nature of reality itself. Want to explore this connection visually? Check out this interactive visualization. For an extensive gallery of Julia Set variations and deeper mathematical insights, visit Paul Bourke’s comprehensive collection.

NOTE: Found a mistake or have feedback? I’d love to hear from you - please reach out via email!